01、数轴上原点两旁，且与原点距离相等的两点所对应的两个数，互称“相反数”。两实数互为相反数的充要条件是它们的和为零。零的相反数仍是零。

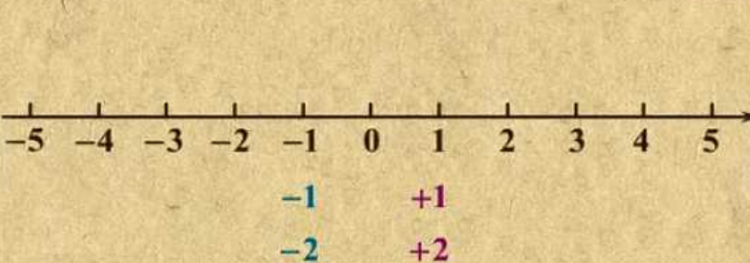
02、只有符号不同的两个数，我们就说其中一个是另一个的相反数，但0的相反数是0。一般地，任意的一个有理数a，它的相反数是-a。a本身既可以是正数，也可以是负数，还可以是零。（具体取法：正数的相反数是数前加负号，负数的相反数是将原数的负号去掉，0的相反数是0）互为相反数的两个数在数轴上表示出来后，表示这两个数的点，分别在原点的两旁，与原点的距离相等，并且互为相反数的两个数的和为0.

03、在一个数的前面添上“－”号就成为原数的相反数。若 表示一个有理数，则 的相反数表示为－ 。在一个数的前面添上“ ”号仍与原数相联系同。例如，＋7=7，特别地，＋0=0，－0=0。

04、多重符号化简
1、相反数的意义是简化多重符号的依据。如 是－1的相反数，而－1的相反数为 1，所以 。
2、多重符号化简的结果是由“－”号的个数决定的。如果“－”号是奇数个，则果为负；如果是偶然数个，则结果为正。可简写为“奇负偶正”。